AP Physics Chapter 9 Full Notes

AP Physics - Chapter 9

Lesson 46: Torque

Notes

LEARNING TARGET & JOURNALS

I can define torque as the ability of a force to cause rotation.

NOTES

Torque is the tendency of a force to rotate an object about an axis.
The magnitude of torque depends on three things:

the force applied
the length of the lever arm

The lever arm is the distance between the application of the force and the rotating axis

the angle at which the force is applied to the lever arm

The torque is the product of the force applied perpendicularly to lever arm and the length of the lever arm itself.

${"backgroundColor":"#ffffff","backgroundColorModified":false,"type":"$$","id":"1-0","aid":null,"font":{"size":"14","family":"Calibri","color":"#000000"},"code":"$$\\tau=rF\\cdot \\sin \\theta$$","ts":1646073577645,"cs":"A5S0/bXGe6eHm8fDHA5HCQ==","size":{"width":105,"height":12}}$

r refers to the length of the lever arm, or distance between the applied force and the axis of rotation.
It is always the sine of the angle between the applied force and the lever arm.

NOTICE: The angle 𝛳 is assumed to be less than 90°.
So the angle must be made with the lever arm, or an imaginary extension of the lever arm.

The variable for torque is the Greek letter tau. ${"backgroundColorModified":false,"code":"$$\\left(\\tau\\right)$$","type":"$$","font":{"size":"12","color":"#000000","family":"Calibri"},"backgroundColor":"#ffffff","id":"2","aid":null,"ts":1646073599259,"cs":"wOHZDwVTpVWtVo6V/zPw2g==","size":{"width":17,"height":16}}$

The SI unit for torque is the Newton·meter. (Nm)

Torque is a vector quantity, so you must include direction.

The direction is determined by the intended rotation created by the force.

A force that would induce a clockwise rotation produces a negative torque.
Thus, a force inducing a counter-clockwise rotation produces a positive torque.

The maximum torque that can be applied is when ${"backgroundColorModified":false,"backgroundColor":"#ffffff","font":{"family":"Calibri","color":"#000000","size":"11"},"code":"$\\theta \\, =\\, 90\\udeg $","type":"$","aid":null,"id":"3","ts":1646073696833,"cs":"pf2g7G4Enmc09Vvtee2p7w==","size":{"width":49,"height":10}}$ , which would cause the so the resulting equation would be ${"font":{"color":"#000000","family":"Calibri","size":"12"},"aid":null,"code":"$$\\tau=rF$$","id":"1","backgroundColor":"#ffffff","backgroundColorModified":false,"type":"$$","ts":1646073643483,"cs":"LSHg9Jo4k95J8IUc9Yq6qA==","size":{"width":48,"height":10}}$
To increase the amount of torque produced without changing the force, then increase the length of the lever arm.

Torque has the same units as work and energy. (1 Nm = 1 J)

However torque is not a measurement of work or energy. So keep the units for torque as Nm to differentiate from work or energy.

EXAMPLE 1 – Find the torque in the following situations.

Find the magnitude of the torque produced by a 3.0 N force applied to a door at a perpendicular distance of 0.25 m from the hinge.

In a canyon between two mountains, a spherical boulder with a radius of 1.4 m is just set in motion by a force of 1600 N. The force is applied at an angle of 53.5° measured with respect to the radius of the boulder. What is the magnitude of the torque on the boulder?

EXAMPLE 2 – Solve using torque.

If the torque required to loosen a nut that holds a wheel on a car has a magnitude of 58 N•m, what force must be exerted at the end of a 0.35 m lug wrench to loosen the nut when the angle is 124°?
If the torque required to loosen a nut on the wheel of a car has a magnitude of 40.0 N•m, what minimum force must be exerted by a mechanic at the end of a 30.0 cm wrench to loosen the nut?
Calculate the net torque about the axle of the wheel shown.
Determine the net torque about point C as the pivot point on the 2.0-m-long uniform beam shown. All forces are shown.

AP Physics - Chapter 9

Lesson 47: First and Second Condition for Equilibrium

Notes

LEARNING TARGET & JOURNALS

I can characterize the Second Condition for Equilibrium.

NOTES

Mechanical equilibrium is defined as a system that experiences no net acceleration.

That now means translational acceleration as well as angular acceleration.

Two conditions must exist for an object to be in equilibrium:

The sum of all forces acting on an object is equal to zero.

This is known as the 1st Condition for Equilibrium or Translational Equilibrium

${"aid":null,"backgroundColorModified":false,"font":{"size":"12","color":"#000000","family":"Calibri"},"backgroundColor":"#ffffff","code":"$$\\sum_{}^{}F_{x}=F_{1x}\\pm\\,F_{2x}\\pm\\,F_{f}\\pm\\,F_{R}\\pm\\,...=0\\,N$$","id":"4","type":"$$","ts":1646074124282,"cs":"/OB5/ZOADwAFhBXj+v2q0Q==","size":{"width":302,"height":22}}$ and ${"code":"$$\\sum_{}^{}F_{y}=F_{1y}\\pm\\,F_{2y}\\pm\\,F_{g}\\pm\\,...=0\\,N$$","id":"4-1","type":"$$","aid":null,"font":{"size":"12","family":"Calibri","color":"#000000"},"backgroundColor":"#ffffff","backgroundColorModified":false,"ts":1646074132223,"cs":"PRQbrwoE4tZb1N84BvR1Eg==","size":{"width":256,"height":21}}$

The sum of all the torques acting on an object is equal to zero.

This is known as the 2nd Condition for Equilibrium or Rotational Equilibrium

${"aid":null,"type":"$$","id":"5-0","backgroundColorModified":false,"code":"$$\\sum_{}^{}\\tau=r_{1}F_{1}\\sin \\theta_{1}\\pm\\,r_{2}F_{2}\\sin \\theta_{2}\\pm\\,r_{g}F_{g}\\pm\\,...=0\\,Nm$$","font":{"size":"12","color":"#000000","family":"Calibri"},"backgroundColor":"#ffffff","ts":1646074253045,"cs":"NNhDlct+9LOAMBMycdqOhg==","size":{"width":372,"height":22}}$

When the object is rotating around itself, the torque created by the weight of the object is 𝜏g = 0 Nm.

Because the force of gravity is acting at the center of gravity which is the pivot point, so r = 0 m.

A system can be one object, it may be multiple objects.

In either case, unless noted otherwise, the pivot point is located at the center of mass for the system.

EXAMPLE 1 – Determine if the following system is in equilibrium.

EXAMPLE 2 - A woman of mass m = 55.0 kg sits on the left end of a seesaw—a plank of uniform length L = 4.00 m, pivoted in the middle as shown.

First compute the torques on the seesaw about an axis that passes through the pivot point. Where should a man of mass M = 75.0 kg sit if the system (seesaw plus man and woman) is to be balanced?

Find the normal force exerted by the pivot if the plank has a mass of mpl = 12.0 kg.

AP Physics - Chapter 9

Lesson 48: Center of Gravity and Stability

Notes

LEARNING TARGET & JOURNALS

I can identify the location of the center of mass for any object or system.

NOTES

The center of mass is defined as the average location of all the mass.

Whereas the center of gravity is the average location of the weight of an object.

Both the CoM and CoG are at the same location when the object is small in size and close in separation relative to the gravitational source.

For example, the center of gravity of the Sears (Willis) Tower in Chicago is about
1 millimeter below its center of mass. (Paul Hewitt, “Conceptual Physics”)

The center of mass, or center of gravity, may or may not lie within the mass of the object itself, but will be located inside the “framework” of the mass, or system of masses.

When studying the rotation of an object, the center of gravity lies on the axis of rotation.

That means the natural pivot point of an object is its center of gravity.

For objects of uniform mass, the center of mass is located at the geometric center of the shape.

So the center of mass of a uniform meter-stick is located at x = 0.50 m.

Therefore, the pivot point for any uniform object is located at its geometric center.

The center of mass of an object is defined as the location where the sum of all the mass equals zero.

It is essentially the average location of all massive points with respect to their distance from a set reference point.

We often agree that the reference point is most commonly the origin of a coordinate plane, but it may be set differently to fit the problem.

For an linear object or system of unequal mass distribution, the center of mass can be calculated by

$<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>x</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub><mo> </mo><mo>=</mo><mo> </mo><mfrac><mrow><msub><mi>m</mi><mn>1</mn></msub><msub><mi>x</mi><mn>1</mn></msub><mo> </mo><mo>+</mo><mo> </mo><msub><mi>m</mi><mn>2</mn></msub><msub><mi>x</mi><mn>2</mn></msub><mo> </mo><mo>+</mo><mo> </mo><mo>.</mo><mo>.</mo><mo>.</mo></mrow><mrow><msub><mi>m</mi><mn>1</mn></msub><mo> </mo><mo>+</mo><mo> </mo><msub><mi>m</mi><mn>2</mn></msub><mo> </mo><mo>+</mo><mo> </mo><mo>.</mo><mo>.</mo><mo>.</mo></mrow></mfrac></math>$

For a two-dimensional object or system of unequal mass distribution, the center of mass is calculated similarly to the method above by averaging each dimension one at a time. $CoM = \left( {\frac{{\sum {{m_i}{x_i}} }}{M},\frac{{\sum {{m_i}{y_i}} }}{M}} \right)$

Where M is the sum of the individual masses.

Simply add another averaging operation for a three-dimensional axis. However, rarely do we study three dimensional systems at this level.

While the center of mass can identify the balance point, and therefore the object’s own axis of rotation, it may or may not split the object itself into two equal masses.

Imagine where the CoM would be for each part of the object after being cut at the CoM.

For non-uniform masses, the heavier mass will have a shorter distance (or lever arm) to its CoM to allow the object to balance properly at the actual CoM of the original object.

Another phenomenon related to the position of the center of gravity is that objects will topple over when their center of gravity is outside of the frame of their base.

That is because its own weight now has a lever arm to create torque with!

EXAMPLE 1 – Identify the point the best represents the center of mass (CM) of the object.

EXAMPLE 2 – Find the center of mass of the given systems.

EXAMPLE 3 – Answer the following in regards to center of mass and stability.

Which truck(s) will topple over on the incline?

▢ A ▢ B ▢ C

The center of gravity of a loaded truck depends on how the truck is packed. If it is 4.0 m high and 2.4 m wide, and its CG is 2.2 m above the ground, how steep a slope can the truck be parked on without tipping over

AP Physics - Chapter 9

Lesson 49: Applications of Equilibrium – Teeter-Totter Problems

Notes

LEARNING TARGET & JOURNALS

I can apply all conditions for equilibrium for teeter-totter type problems.

NOTES

A common family of problems used to study rotational equilibrium use teeter-totters.
These can usually be solved by satisfying the 2nd Condition of Equilibrium by summing the torques to zero.

${"backgroundColor":"#ffffff","id":"5-1","code":"$$\\sum_{}^{}\\tau=r_{1}F_{1}\\sin \\theta_{1}\\pm\\,r_{2}F_{2}\\sin \\theta_{2}\\pm\\,\\left(0\\,m\\right)F_{g}\\pm\\,\\left(r_{object}\\right)\\left(F_{g,object}\\right)=0\\,Nm$$","backgroundColorModified":false,"font":{"size":"12","family":"Calibri","color":"#000000"},"aid":null,"type":"$$","ts":1646074393542,"cs":"hmykoOZ/likpF1KuOe1DUg==","size":{"width":490,"height":22}}$

Notice, the forces here are typically just weights, which are most likely perpendicular to the lever arm, so no need for sin θ.
When finding where to place an object to bring the system to equilibrium

make your best guess on which side to put the object on and call that distance away from the pivot point x.
Use the overall length of the structure to establish the remaining distances as (L – x).
Set the counterclockwise torques equal to the clockwise torques and solve for x.

If your answer is negative, then the distance is correct but the object should be on the other side of the pivot.

EXAMPLE 1 – Determine where a child should be put to bring the system to equilibrium.

Three children are trying to balance on a seesaw, which includes a fulcrum rock acting as a pivot at the center, and a very light board 3.2 m long. Two playmates are already on either end. Boy A has a mass of 45 kg, and boy B a mass of 35 kg. Where should girl C, whose mass is 25 kg, place herself so as to balance the seesaw?

EXAMPLE 2 – A 75-kg adult sits at one end of a 9.0-m-long board. His 25-kg child sits on the other end.

1. Where should the pivot be placed so that the board is balanced, ignoring the board’s mass?

2. Find the pivot point if the board is uniform and has a mass of 15 kg.

AP Physics - Chapter 9

Lesson 50: Applications of Equilibrium – Bridge & Scaffold Problems

Notes

LEARNING TARGET & JOURNALS

I can apply all conditions for equilibrium for bridge/scaffold type problems.

NOTES

Another common type of problem to illustrate equilibrium is to place a car on a bridge or a person on a platform supported by two wires.
When drawing the free-body diagram, be sure to draw:

The weight of the bridge in the middle of the bridge.
A force for each supporting structure/cable typically pointed upward.
A weight vector for any extra object (car/person/etc) on the bridge.

To solve for the unknown forces of the supporting objects you will need to use both conditions of equilibrium:

First apply the 2nd Condition of Equilibrium using one of the supporting forces as the pivot point.

Substitute the now known supporting force into the 1st Condition of Equilibrium.

${"type":"$$","id":"6","backgroundColorModified":false,"aid":null,"code":"$$\\sum_{}^{}F_{y}=F_{1}+F_{2}-F_{g}-F_{g,\\,object}=0\\,N$$","backgroundColor":"#ffffff","font":{"family":"Calibri","size":"12","color":"#000000"},"ts":1646074633064,"cs":"ln/bewjmwDFwctnr/DEDkw==","size":{"width":272,"height":22}}$

EXAMPLE 1 – A uniform bridge 20.0 m long and weighing 4.00 × 105 N is supported by two pillars located 3.00 m from each end. If a 1.96 × 104 N car is parked 8.00 m from one end of the bridge, how much force does each pillar exert?

EXAMPLE 2 - A uniform plank of length 2.00 m and mass 30.0 kg is supported by three ropes, as in the figure below. Find the tension in each rope when a 700-N person is 0.500 m from the left end.

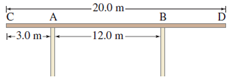
EXAMPLE 3 – A 20.0-m-long uniform beam weighing 650 N rests on walls A and B.

Find the maximum weight of a person who can walk to the extreme end D without tipping the beam.
Find the forces that the walls A and B exert on the beam when the person is standing at D.

AP Physics - Chapter 9

Lesson 51: Applications of Equilibrium – Pivot Point Not @ CG

Notes

LEARNING TARGET & JOURNALS

I can assess a system in equilibrium with a fixed pivot point.

NOTES

The most common type of these problems involves a weighted object hanging from a lever arm that is attached to a wall at one end with/without supporting cables.

Use the attachment to the wall as the pivot point in this case.

To solve for the tension in the supporting cable

solve for the tension by satisfying the 2nd Condition of Equilibrium.

${"code":"$$\\sum_{}^{}\\tau=\\left(r_{tension}\\right)F_{T}\\sin \\theta\\pm\\,\\left(r_{CM}\\right)F_{g,beam}\\pm\\left(r_{object}\\right)F_{g,object}=0\\,Nm$$","type":"$$","font":{"color":"#000000","size":"12","family":"Calibri"},"aid":null,"backgroundColorModified":false,"id":"7","backgroundColor":"#ffffff","ts":1646074780262,"cs":"EbVU1MfPyTUGJ49Asz6wig==","size":{"width":456,"height":22}}$

Notice the force vector for the weight of the bar acts at a point away from the pivot point, so the torque it creates must be accounted for now.

If asked to find the force provided by the supporting wall, you will then need to apply the 1st Condition of Equilibrium in both dimensions due to the supporting cable being at an angle.

The horizontal force provided by the wall is equal to the horizontal component of the tension. ${"id":"8","backgroundColorModified":false,"type":"$$","code":"$$\\sum_{}^{}F_{x}=F_{Tx}\\pm F_{x,wall}=0\\,N$$","backgroundColor":"#ffffff","aid":null,"font":{"color":"#000000","family":"Calibri","size":"11"},"ts":1646076190989,"cs":"BdERU2y+zhid4yqV/1KNEw==","size":{"width":181,"height":20}}$
Remember, the wall must also provide a vertical force upward. ${"backgroundColorModified":false,"type":"$$","id":"8","font":{"family":"Calibri","size":"11","color":"#000000"},"aid":null,"code":"$$\\sum_{}^{}F_{y}=F_{Ty}\\pm F_{y,wall}\\pm F_{g,beam}\\pm F_{g,object}=0\\,N$$","backgroundColor":"#ffffff","ts":1646076278181,"cs":"A+GXRiG0wwnezV12iuh+NQ==","size":{"width":304,"height":20}}$
The overall force provided by the wall must be found by Pythagorean Theorem using the vertical and horizontal supporting forces found to satisfy the
1st Condition of Equilibrium. ${"backgroundColor":"#ffffff","type":"$$","id":"9","aid":null,"font":{"color":"#000000","family":"Calibri","size":"10"},"code":"$$F_{wall}={\\sqrt[]{\\left(F_{x,wall}\\right)^{2}+\\left(F_{y,wall}\\right)^{2}}}$$","backgroundColorModified":false,"ts":1646077111344,"cs":"an5/kJZYH01oK7tPN4doFg==","size":{"width":176,"height":24}}$

We can use both conditions of equilibrium now to find the force of friction exerted by a leaning structure like a ladder.

To calculate the torques, you will want to treat the end of the ladder in contact with the ground as an attached pivot point.

So the weight of the uniform ladder will now create torque with a lever arm length of half the ladder.
As will the weight of the person on the ladder.

The lever arm is the distance up the ladder of the person.

As will the normal force provided by the wall at the other end of the ladder with a lever arm as the entire length of the ladder.

The forces applied to the lever arm at an angle can be determined using angle pair relationships from Geometry with the base angle of the ladder and the ground.
Each condition of equilibrium plays a vital role in our observations.

Summing the net vertical forces will find the normal force exerted by the ground on the ladder.

${"font":{"family":"Calibri","color":"#000000","size":"11"},"code":"$$\\sum_{}^{}F_{y}=F_{N,ground}-F_{g,ladder}-F_{g,person}=0\\,N$$","aid":null,"backgroundColor":"#ffffff","id":"8-0","type":"$$","backgroundColorModified":false,"ts":1646077550337,"cs":"9Ab1pBGh8ZV8NmaK2jr9+w==","size":{"width":289,"height":20}}$

All the ground has to do is hold up the weight of the ladder and the person on the ladder.

Summing the net torques is usually necessary to find the normal force provided by the wall on the ladder.

${"backgroundColor":"#ffffff","font":{"size":"11","color":"#000000","family":"Calibri"},"code":"$$\\sum_{}^{}\\tau=\\left(L\\right)F_{N,wall}\\sin \\theta \\pm \\left(\\frac{L}{2}\\right)F_{g,ladder}\\sin\\left(90-\\theta\\right)\\pm \\left(r_{person}\\right)F_{g,person}\\sin\\left(90-\\theta\\right)=0\\,Nm$$","backgroundColorModified":false,"aid":null,"type":"$$","id":"8-1","ts":1646077899465,"cs":"mrhCAZkvC7GUoHBXtJhN6Q==","size":{"width":572,"height":36}}$

Since the ladder is “attached” to the ground, the wall is responsible for keeping it from rotating.

Summing the net horizontal forces will find you the force of friction so the ladder does not slide out.

${"type":"$$","aid":null,"backgroundColorModified":false,"backgroundColor":"#ffffff","code":"$$\\sum_{}^{}F_{x}=F_{f}-F_{N,wall}=0\\,N$$","id":"8","font":{"family":"Calibri","color":"#000000","size":"11"},"ts":1646078046705,"cs":"PN5cU9qnvZ1vd6JukwXVJw==","size":{"width":177,"height":20}}$

You have to find the force from the wall in order to find the force of friction at the base of the ladder.

EXAMPLE 1 – A uniform 5.00 m long horizontal beam that weighs 315 N is attached to a wall by a pin connection that allows the beam to rotate. Its far end is supported by a cable that makes an angle of 53° with the horizontal, and a
545 N person is standing 1.50 m from the pin. Assume the beam is in equilibrium.

Find the force in the cable, FT.

Find the vertical component of the force exerted on the beam by the wall.

Find the horizontal component of the force exerted on the beam by the wall.

Find the magnitude of the total exerted on the beam by the wall, R.

EXAMPLE 2 - A uniform ladder 10.0 m long and weighing 50.0 N rests against a smooth vertical wall as shown. If the ladder is just on the verge of slipping when it makes a 50.0° angle with the ground,

Find the force provided by the wall to hold the ladder, P.

Find the coefficient of static friction between the ladder and ground.